Risk-adjusted NPV is Notoriously Fallible
Over at least the past decade, risk-adjusted Net Present Value (rNPV) has emerged as the de facto standard for valuing pharmaceutical R&D projects (1,2). These valuations are used for several purposes including prioritizing projects within a portfolio, making investment decisions, valuing a licensing transaction and valuing intellectual property in a sale setting. The approach is based on standard discounted cash flow (DCF) techniques with future cash flows weighted by the probability of a drug progressing from one development stage to the next. Controversies remain, not least the choice of discount rate to apply, but the methodology remains very widely used, at least in Big Pharma and those biotech companies that have not lost faith in rNPV. In a context of high – and often unquantifiable – uncertainties inherent on pharmaceutical R&D and market forecasting (3), it is known that DCF and even rNPV techniques provide “misplaced concreteness” whereby “the tendency to overlook uncertainties, margins of error and ranges of probability can lead to damaging misjudgements” (4). Superimposing Monte Carlo (MC) simulations on to rNPV calculations provides explicit recognition of this and results in an rNPV expressed as a range associated with a specific probability distribution. This paper briefly documents an alternative risk-profiled MC rNPV valuation (rpNPV), and highlights a material divergence between the perspective of a biotech company (with a single or small number of projects) and Big Pharma (with a broad portfolio).
Conventional r-NPV Valuation with Monte Carlo Simulations (Standard MC Model)
As a practical illustration, consider a novel therapeutic for non-small cell lung cancer (NSCLC) starting Phase I clinical trials with the basic assumptions as set out in Table 1; while uncertainties, especially commercial ones, are very high and reflected by wide input ranges. The probability of progressing from one development stage to the next, using benchmarks that have been widely used in the industry (5), are assumed to be:
- Phase I to Phase II trials: 71%
- Phase II to Phase III trials: 45%
- Phase III trials to pre-registration: 64%
- Pre-registration to product approval: 93%
Cumulatively, the probability of technical success, from preclinical development through to product approval, is 19%; many would argue this is overoptimistic relative to contemporary experience, especially in a challenging indication such as NSCLC, but the analysis presented below holds with more stringent benchmarks based on success rates in specific indications and with different technologies (small molecules, biologics, etc.) (6) (data not shown). In the standard rNPV model, the net cash flow is multiplied by the cumulative probabilities at each stage; i.e. all cash flows from Phase I to Phase II are multiplied by 0.71, from Phase II to Phase III by 0.71 x 0.45 = 0.32, etc. The formal calculation of rNPV uses a familiar standard algorithm (7). Using the midpoint values for all the ranges specified in Table 1, at a discount rate of 8% the rNPV = $485 million. Using the MC method, this calculation is repeated many times (in this example, 50,000 times) using a Microsoft Excel spreadsheet plug-in (Model Risk 5, Vose Software BVBA), each run using a different value in each of the assumption ranges in Table 1. These 50,000 simulations effectively sample the range of possible outcomes based on an appropriate probability distribution for each input variable (for most variables, this model used a PERT distribution (8)).
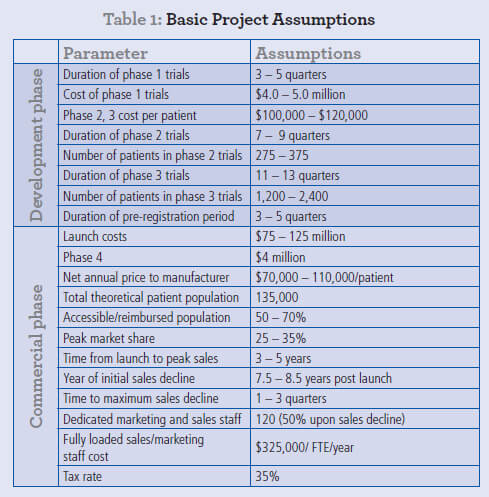
The mean rNPV from these simulations is $484 million, effectively identical to the non-MC value. More importantly, the range of rNPV values is shown in a histogram plot (Fig. 1a), with the 5th and 95th percentiles for rNPV respectively being $357 million and $627 million. This probability distribution provides a far richer insight into the rNPV associated with this early-stage R&D project. In this example, all values in the range are positive, but for projects where the commercial target is smaller or the uncertainties higher (data not shown), the first quartile of even more of the rNPV range can be negative despite a positive mean rNPV, clearly providing a more accurate view of the risks involved in pharmaceutical R&D. More importantly still, the relative impact of each range of input assumptions on the outcome of the rNPV calculation is shown in a Tornado plot (Fig. 1b).
Consistent with conventional wisdom, the assumptions with the greatest impact on valuation are:
- Price
- Peak market share
- Accessible market (i.e. the available market taking into account clinical, payer and other restrictions on eligibility for treatment)
Assumptions such as the cost of clinical trials, even Phase III, have a significantly lower impact on rNPV. It is precisely this sort of analysis that led many in the industry, certainly up to ca. 2005, to focus very heavily on commercial parameters and to invest heavily in clinical development with relatively scant regard for R&D budgets.
While it provides an illustration of the potential spread of project NPVs and the assumptions that the greatest impact on the range, the MC rNPV method still masks the reality of the situation where projects more often fail than succeed. As a result it has less utility in decision-making than stringent use of MC methods can provide.
Overcoming the Limitations of the Conventional Approach Using a Stringent MC Model
The fundamental problem with the standard rNPV method is that it applies a probability weighting to cash flows according to transitions through key development hurdles, e.g. it calculates 71% of cash flows from Phase I to Phase II. In reality, however, there is no such thing as 71% of a cash flow; instead, 29% of the scenarios result in no cash flow beyond Phase I (as the trial yielded a negative result), and 71% of the scenarios resulted in a full, not partial, cash flow between Phase I and Phase II. To better reflect real-life scenarios, we use a stringent MC model: simulations are run in which 71% proceed beyond Phase I, of which 45% proceed beyond Phase II, of which 64% proceed beyond Phase III, etc. Only 19% of the scenarios have cash flows beyond the pre-registration phase, consistent with the overall probability of the product reaching the market; 81% of the scenarios have negative rNPV.
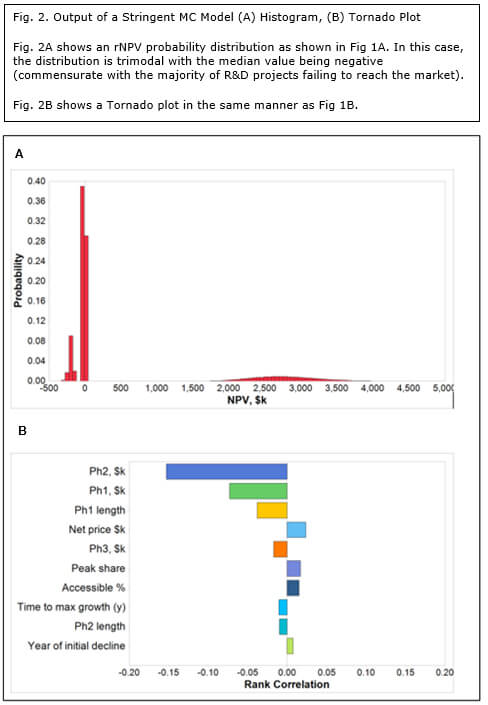Using the same project assumptions, the mean rNPV is still $484 million, but the shape of the histogram is radically different (Fig 2a). In this case, the probability distribution is trimodal; at the 5th percentile with an rNPV of -$202 million, at the 15th percentile with an rNPV of -$34 million and at the 90th centile with an rNPV of $2.7 billion. The first peak corresponds to a late-stage development failure. By far the highest peak (the most probable outcome) is the middle one, corresponding to an outcome of a modest loss on a project cancelled at a relatively early stage. The third peak, with a very high valuation is clearly the least probable and reflects a successfully launched new product. This model is materially more representative of the economics of drug development than Method 1 and can therefore arguably claim higher validity. It is not in common use possibly due to the lack of MC simulation expertise and culture within the pharmaceutical and biotech industries.
It is the Tornado plot for the stringent MC method that provides a fascinating dichotomy (Fig. 2b). In contrast to the standard method, commercial assumptions such as price, market share and market access pale in relation to development parameters, namely:
- Cost of Phase II trials
- Cost of Phase I trials
- Length of Phase I trials
Given that early development is where most projects fail, it is not surprising that these parameters have the highest impact on valuation. Interestingly, biotechs tend to be much better at minimizing costs and time of early phase clinical trials than Big Pharma.
Risk-profiled NPV
Using the stringent MC method, the shape of the rNPV histogram, together with the parameters of the Tornado plot, constitute a risk-profiled NPV model (rpNPV) which is more representative of the reality of life sciences R&D than standard rNPV values.
The standard method may be germane to a biotech company focusing on a single product or perhaps a small portfolio. It is particularly useful in situations addressing a single asset, such as a partnering transaction, where the Monte Carlo analysis constitutes a systematic, multi-parameter sensitivity analysis. In these situations, the histogram plot output makes explicit the range of value encompassed by the uncertainty in the input assumptions, and the Tornado plot identifies which assumptions contribute most to this uncertainty. This can be useful to focus negotiations onto key parameters rather than those which have little or no effect on the ultimate rNPV number used as the basis for the transaction. It can also be important to guide further analysis and/or market research onto parameters where a narrowing of the input assumption ranges would significantly reduce the uncertainty in the valuation.
However, the probability distribution of the rNPV range using the standard approach does not reflect reality and is materially and consistently overoptimistic. The rpNPV (stringent method), however, reflects the dynamics of a large portfolio of the type present in major integrated pharmaceutical firms or venture capital investors. The standard rNPV approach does not serve portfolio management well as it always favours short-term and incremental projects at the expense of early stage and strategic projects. Instead, an rpNPV approach should be used to make trade-offs between projects within a portfolio.
Beyond this, a possible message from the rpNPV model is that Big Pharma should pay maximum attention to containing the costs and duration of early development phases as these have a higher economic impact in the context of a broad portfolio than optimizing post-launch commercial parameters for individual products although, obviously, these are not unimportant. A corollary is that it may be economically most efficient for Big Pharma not to conduct early development at all, rather it would maximize shareholder value to acquire products that have already successfully navigated Phase II proof-of-concept clinical trials; indeed, many are already some way down this path as they increasingly outsource R&D.
The rpNPV model provides much greater insight/transparency into the dynamics driving project returns, enabling more effective comparison between alternative development paths for a project and between different projects competing for resources where they may have similar standard rNPVs but radically different risk profiles. As such it is a valuable decision-making tool for modern portfolio management.
References
1 Bogdan, B. & Villiger, R., Valuation in Life Sciences 3rd Ed., doi 10.1007/978-3-642-10820-4_2, Springer-Verlag Berlin Heidelberg (2010)
2 Svennebring, A.M. & Wikberg, A.E.S. Net present value approaches for drug discovery Springerplus doi 10.1186/2193-1801-2-140 (2013)
3 Cha, M., Rifai, B. & Sarraf, P. Pharmaceutical forecasting: throwing darts? Nat Reviews Drug Discovery 12, 737–738 (2013)
4 Savage, S.L., The Flaw of Averages, John Wiley & Sons, Inc. (2012)
5 DiMasi, J.A., Feldman, L., Seckler, A. & Wilson, A. Trends in risks associated with new drug development: success rates for investigational drugs. Clin. Pharmacol. Ther. 87, 272–277 (2010).
6 Hay, M., Thomas, D.W., Craighead, J.L., Economides, C. & Rosenthal, J.. Clinical development success rates for investigational drugs. Nat Biotechnol. 32, 40–51 (2014)
7 Stewart, J.J., Allison, P.N., Johnson, R.S. Putting a price on biotechnology Nat Biotechnol. 19, 813-7 (2001)
8 Vose, D. Risk Analysis, a Quantitative Guide, 3rd Ed. John Wiley & Sons Ltd (2008)
Download a PDF version:
Pharma and Biotech Valuations, Anthony Walker et al, Alacrita, July 2015